카누누카
(C) 자료구조 - 연결 리스트의 응용 및 구현 본문
1. 단순 연결 리스트를 이용한 다항식 표현
- 다항식에 있는 항 하나는 노드 하나로 표현한다.
- 각 항마다 계수와 지수를 저장해야하므로 노드의 데이터 필드는 계수를 저장하는 coef와 지수를 저장하는 expo 필드로 구성하고, 링크 필드는 다음 항을 연결하는 포인터로 구성한다.

<다항식 노드의 구조체 정의>
|
1
2
3
4
5
|
typedef struct Node {
float coef;
int expo;
struct Node *link;
};
|
cs |
<다항식 A(x)와 B(x)의 단순 연결 리스트 표현>

A(x) = 4x^3 + 3x^2 + 5x
B(x) = 3x^4 + x^3 + 2x + 1
2. 다항식 연결 자료구조의 항 삽입 알고리즘
- 다항식에 항을 추가하려면 연결 리스트의 마지막 노드 다음에 새로운 노드를 추가하는 알고리즘으로 정의할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
// 다항식 리스트에 마지막 노드를 추가하는 연산
void appendTerm(ListHead* L, float coef, int expo) {
ListNode* newNode;
ListNode* p;
newNode = (ListNode*)malloc(sizeof(ListNode));
newNode->coef = coef;
newNode->expo = expo;
newNode->link = NULL;
if (L->head == NULL) { // 다항식 리스트가 공백인 경우
L->head = newNode;
return;
}
else { // 다항식 리스트가 공백이 아닌 경우
p = L->head;
while (p->link != NULL) {
p = p->link; // 리스트의 마지막 노드를 찾음
}
p->link = newNode; // 새 노드 연결
}
}
|
cs |
3. 다항식끼리의 덧셈 연산과 알고리즘
- A(x) + B(x) = C(x)를 단순 연결 리스트 자료구조를 사용하여 해결하는 방법
1) 포인터 p : 다항식 A(x)에서 비교할 항
2) 포인터 q : 다항식 B(x)에서 비교할 항
3) 포인터 r : 덧셈 연산을 마친 C(x)의 항을 지시
- 다항식 A(x) 항의 지수(p.expo)와 다항식 B(x)의 항의 지수(q.expo)를 비교하여 세 가지 경우로 처리
1) p.expo < q.expo : 다항식 A(x) 항의 지수가 작은 경우
두 다항식의 지수가 다르면 계수를 더할 수 없고, 지수가 높은 항부터 나열하는 다항식 표현 규칙에 따라서 포인터 q가 다항식 B(x) 항을 C(x) 항으로 복사한다.
2) p.expo == q.expo : 두 다항식 항의 지수가 같은 경우
p.coef와 q.coef를 더해 C(x) 항인 r.coef에 저장하고, 지수는 p.expo(또는 q.expo)를 r.expo에 저장한다. 그리고 다음 항을 비교하기 위해 포인터 p와q를 각각 노드로 이동시킨다.
3) p.expo > q.expo : 다항식 A(x) 항의 지수가 큰 경우
p가 가리키는 A(x) 항의 지수가 더 크면 포인터 p가 가리키는 항을 C(x) 항으로 복사한다. 포인터 p가 가리키는 항에 대한 처리가 끝났으므로 p를 다음 노드로 이동시킨다.
-> 다항식의 모든 항이 처리되어 포인터 p와q가 모드 NULL이 되면 덧셈 연산은 종료된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// 두 다항식의 덧셈을 구하는 연산
void addPoly(ListHead* A, ListHead* B, ListHead* C) {
ListNode* pA = A->head;
ListNode* pB = B->head;
float sum;
// 두 다항식에 노드가 있는 동안 반복 수행
while (pA && pB) {
// 다항식 A의 지수가 다항식 B의 지수와 같은 경우
if (pA->expo == pB->expo) {
sum = pA->coef + pB->coef;
appendTerm(C, sum, pA->expo);
pA = pA->link; pB = pB->link;
}
// 다항식 A의 지수가 다항식 B의 지수보다 큰 경우
else if (pA->expo > pB->expo) {
appendTerm(C, pA->coef, pA->expo);
pA = pA->link;
}
// 다항식 A의 지수가 다항식 B의 지수보다 작은 경우
else {
appendTerm(C, pB->coef, pB->expo);
pB = pB->link;
}
}
// 다항식 A에 남아 있는 노드 복사
for (; pA != NULL; pA = pA->link)
appendTerm(C, pA->coef, pA->expo);
// 다항식 B에 남아 있는 노드 복사
for (; pB != NULL; pB = pB->link)
appendTerm(C, pB->coef, pB->expo);
}
|
cs |
4. 연결리스트를 이용한 다항식 프로그램
- 연결 리스트를 이용해 다항식 덧셈하기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include "LinkedPoly.h"
void main(void) {
ListHead* A, * B, * C;
// 공백 다항식 리스트 A, B, C 생성
A = createLinkedList();
B = createLinkedList();
C = createLinkedList();
appendTerm(A, 4, 3); // 다항식 리스트 A에 4x^3 노드 추가
appendTerm(A, 3, 2); // 다항식 리스트 A에 3x^2 노드 추가
appendTerm(A, 5, 1); // 다항식 리스트 A에 5x 노드 추가
printf("\nA(x) =");
printPoly(A); // 다항식 리스트 A 출력
appendTerm(B, 3, 4); // 다항식 리스트 B에 3x^4 노드 추가
appendTerm(B, 1, 3); // 다항식 리스트 B에 x^3 노드 추가
appendTerm(B, 2, 1); // 다항식 리스트 B에 2x 노드 추가
appendTerm(B, 1, 0); // 다항식 리스트 B에 x^0 노드 추가
printf("\nB(x) =");
printPoly(B); // 다항식 리스트 B 출력
addPoly(A, B, C); // 다항식의 덧셈 연산 수행
printf("\nC(x) =");
printPoly(C); // 다항식 리스트 C 출력
getchar(); return 0;
}
|
cs |
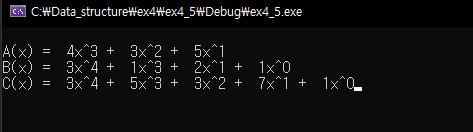
'자료구조' 카테고리의 다른 글
| (C) 자료구조 - 스택의 응용 (4) | 2023.10.23 |
|---|---|
| (C) 자료구조 - 스택의 이해 (6) | 2023.10.17 |
| (C) 자료구조 - 이중 연결 리스트의 구조와 구현 (2) | 2023.10.16 |
| (C) 자료구조 - 원형 연결 리스트의 구조와 구현 (0) | 2023.10.16 |
| (C) 자료구조 - 연결 자료구조와 단순 연결 리스트의 구조와 구현 (2) | 2023.10.13 |




