(C) 자료구조 - 스택의 이해
1. 스택의 개념과 구조
스택(Stack) 자료구조는 접시에 음식을 쌓아올리듯 데이터를 차곡차곡 쌓아올린 형태로 자료를 구성한다.
스택은 같은 구조와 같은 크기의 데이터를 정해진 방향으로만 쌓을 수 있고, top으로 정한 한 곳으로만 접근하도록 제한되어 있다. 따라서 top을 통해 들어온 데이터가 일정한 방향, 즉 아래(Bottom)에서 위로 차곡차곡 쌓이게 된다.
- top
스택에서 유일하게 액세스가 허용된 지점으로 삽입과 삭제가 일어나는 위치이며 현재 스택의 가장 위에 있는 데이터 위치가 된다.
새로 삽입되는 데이터가 스택에서 가장 위에 있는 데이터가 된다.
스택에서 자료를 삭제할 때 top을 통해서만 가능하기 때문에 top에 있는 데이터, 즉 가장 위에 있는 데이터가 삭제되고 삽입된다.
이러한 스택의 동작 구조를 후입선출(LIFO:Last-In-First-Out)이라고 한다.
- 스택의 구조
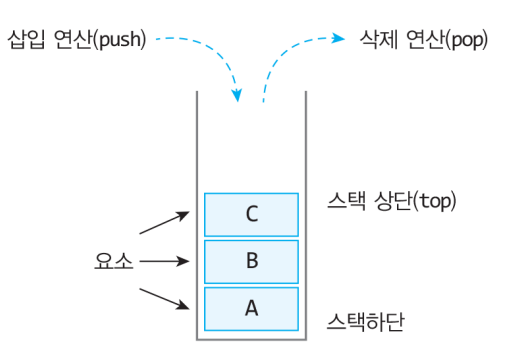
- 스텍의 데이터 삽입(push)과 삭제(pop) 과정

-> 스택에서 데이터가 삽입되고 삭제되는 순서를 결정하는 LIFO 구조는 반드시 지켜져야 한다.
-> 스택의 LIFO 동작 특성으로 인해 스택에서의 삭제 순서는 삽입 순서의 역순이 된다.
2. 스택의 구현
|
1
2
3
4
|
#define STACK_SIZE 100
typedef int element; // 스택 원소(element)의 자료형을 int로 정의
element stack[STACK_SIZE]; // 1차원 배열 스택 선언
|
cs |
- 스택이 공백 상태인지 확인하는 연산
|
1
2
3
4
5
|
// 스택이 공백 상태인지 확인하는 연산
int isStackEmpty(void) {
if (top == -1) return 1;
else return 0;
}
|
cs |
- 스택이 포화 상태인지 확인하는 연산
|
1
2
3
4
5
|
// 스택이 포화 상태인지 확인하는 연산
int isStackFull(void) {
if (top == STACK_SIZE - 1) return 1;
else return 0;
}
|
cs |
2-1. 스택의 원소 삽입
|
1
2
3
4
5
6
7
8
|
// 스택의 top에 원소를 삽입하는 연산
void push(element item) {
if (isStackFull()) { // 스택이 포화 상태인 경우
printf("\n\n Stack is FULL! \n");
return;
}
else stack[++top] = item; // top을 증가시킨 후 현재 top에 원소 삽입
}
|
cs |
2-2. 스택의 원소 삭제
|
1
2
3
4
5
6
7
8
|
// 스택의 top에서 원소를 삭제하는 연산
element pop(void) {
if (isStackEmpty()) { // 스택이 공백 상태인 경우
printf("\n\n Stack is Empty!!\n");
return 0;
}
else return stack[top--]; // 현재 top의 원소를 삭제한 후 top 감소
}
|
cs |
2-3. 스택의 원소 검색
|
1
2
3
4
5
6
7
8
|
// 스택의 top 원소를 검색하는 연산
element peek(void) {
if (isStackEmpty()) { // 스택이 공백 상태인 경우
printf("\n\n Stack is Empty !\n");
return 0;
}
else return stack[top]; // 현재 top의 원소 확인
}
|
cs |
2-4. 스택의 원소 출력
|
1
2
3
4
5
6
7
8
|
// 스택의 원소를 출력하는 연산
void printStack(void) {
int i;
printf("\n STACK [");
for (i = 0; i <= top; i++)
printf("%d ", stack[i]);
printf("] ");
}
|
cs |
- 순차 자료구조를 이용해 순차스택 구현하기 -> 배열 연산을 사용
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include <stdio.h>
#include "stackS.h"
int main(void) {
element item;
printf("\n** 순차 스택 연산 **\n");
printStack();
push(1); printStack(); // 1 삽입
push(2); printStack(); // 2 삽입
push(3); printStack(); // 3 삽입
item = peek(); printStack(); // 현재 top의 원소 출력
printf("peek => %d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d\n", item);
getchar(); return 0;
}
|
cs |

3. 연결 자료구조를 이용한 스택의 구현
순차 자료구조를 이용한 스택은 1차원 배열 변수를 선언하여 쉽게 구현할 수 있다. 하지만, 물리적으로 고정된 배열을 사용하기 때문에 사용 중에 스택의 크기 변경이 어려우므로 배열 크기를 미리 크게 할당해 놓기 때문에 메모리 사용의 효율성이 떨어지는 문제가 생긴다. -> 해결방법 : 연결 자료구조 사용
- 단순 연결 리스트를 이용한 연결 스택 구현
-> 스택의 원소는 연결 리스트의 노드가 된다.
-> 스택에 원소를 삽입할 때마다 연결 리스트에 노드를 하나씩 연결한다.
-> 스택 원소의 순서는 연결 리스트 노드의 링크를 사용하여 표현한다.
-> 스택의 top을 표현하기 위해 포인터 top을 사용한다.
-> 스택의 초기 상태(공백 스택)는 포인터 top을 NULL 포인터로 설정하여 표현한다.
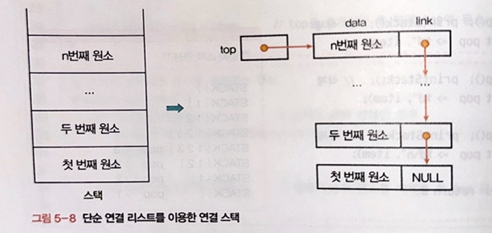
- 연결 자료구조를 이용해 연결 스택 구현하기
|
1
2
3
4
5
6
7
8
|
typedef int element; // 스택 원소(element)의 자료형을 int로 정의
typedef struct stackNode { // 스택의 노드를 구조체로 정의
element data;
struct stackNode* link;
} stackNode;
stackNode* top; // 스택의 top 노드를 지정하기 위해 포인터 top 선언
|
cs |
- 스택이 공백 상태인지 확인하는 연산
|
1
2
3
4
5
|
// 스택이 공백 상태인지 확인하는 연산
int isStackEmpty(void) {
if (top == NULL) return 1;
else return 0;
}
|
cs |
3-1. 스택의 top에 원소를 삽입하는 연산
|
1
2
3
4
5
6
7
8
|
// 스택의 top에 원소를 삽입하는 연산
void push(element item) {
stackNode* temp = (stackNode*)malloc(sizeof(stackNode));
temp->data = item;
temp->link = top; // 삽입 노드를 top의 위에 연결
top = temp; // top 위치를 삽입 노드로 이동
}
|
cs |
3-2. 스택의 top에서 원소를 삭제하는 연산
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// 스택의 top에서 원소를 삭제하는 연산
element pop(void) {
element item;
stackNode* temp = top;
if (isStackEmpty()) { // 스택이 공백 리스트인 경우
printf("\n\n Stack is empty !\n");
return 0;
}
else { // 스택이 공백 리스트가 아닌 경우
item = temp->data;
top = temp->link; // top 위치를 삭제 노드 아래로 이동
free(temp); // 삭제된 노드의 메모리 반환
return item; // 삭제된 원소 반환
}
}
|
cs |
3-3. 스택의 top에 원소를 검색하는 연산
|
1
2
3
4
5
6
7
8
9
10
|
// 스택의 top 원소를 검색하는 연산
element peek(void) {
if (isStackEmpty()) { // 스택이 공백 리스트인 경우
printf("\n\n Stack is empty !\n");
return 0;
}
else { // 스택이 공백 리스트가 아닌 경우
return(top->data); // 현재 top의 원소 반환
}
}
|
cs |
3-4. 스택의 원소를 top에서 bottom 순서로 출력하는 연산
|
1
2
3
4
5
6
7
8
9
10
|
// 스택의 원소를 top에서 bottom 순서로 출력하는 연산
void printStack(void) {
stackNode* p = top;
printf("\n STACK [ ");
while (p) {
printf("%d ", p->data);
p = p->link;
}
printf("] ");
}
|
cs |
- 연결 스택 연산 예제 -> 포인터 연산을 사용
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <stdio.h>
#include "stackL.h"
int main(void) {
element item;
top = NULL;
printf("\n** 연결 스택 연산 **\n");
printStack();
push(1); printStack(); // 1 삽입
push(2); printStack(); // 2 삽입
push(3); printStack(); // 3 삽입
item = peek(); printStack(); // 현재 top의 원소 출력
printf("peek = > % d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d", item);
item = pop(); printStack(); // 삭제
printf("\t pop => %d", item);
getchar(); return 0;
}
|
cs |
